分子動理論方式簡介
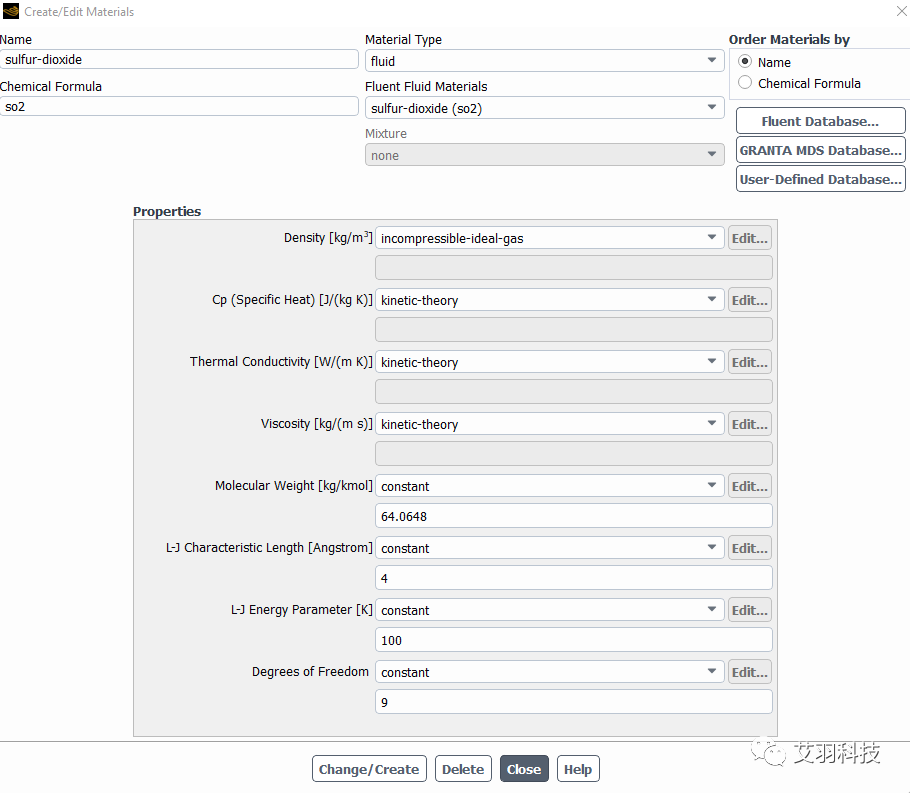
純氣體的設置
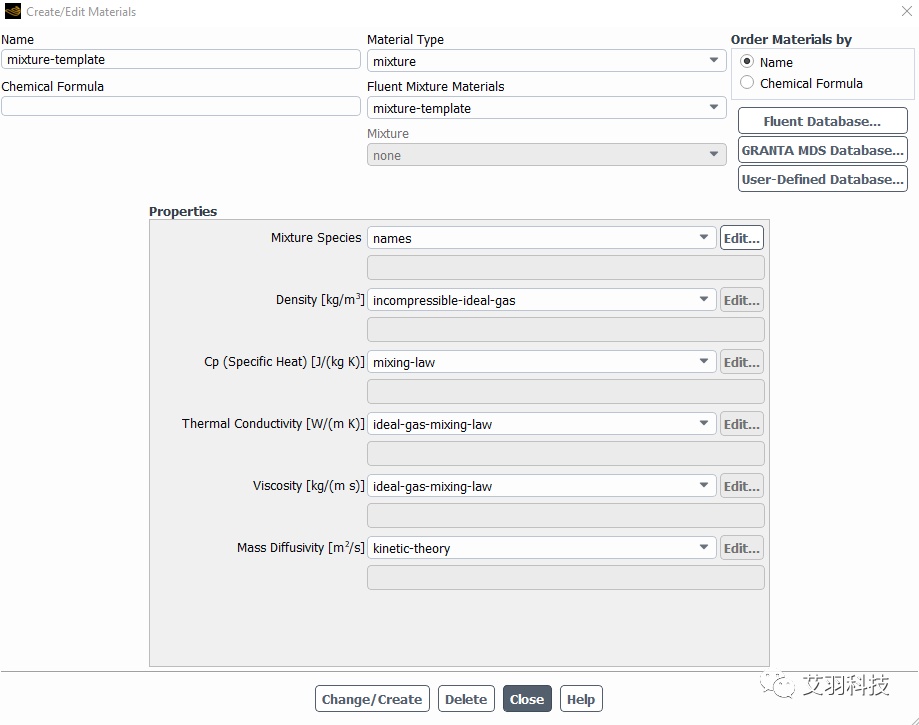
氣體混合物的設置
分子動理論方式無需輸入各類宏觀的材料屬性數(shù)據(jù),適用于氣體介質存在溫度變化很大、組分數(shù)量極多等屬性數(shù)值變化較大、難以查找具體屬性數(shù)值的復雜情況。液體的分子間作用機理遠比氣體復雜,因此不推薦使用分子動理論方法進行材料屬性定義。
采用分子動理論定義材料屬性,前提條件為密度采用理想氣體方式定義,ideal gas law和incompressible ideal gas law均可,這兩種密度定義方式的差異具體可參考Fluent幫助文檔。需要輸入的數(shù)據(jù)包括分子量、L-J特征長度、L-J能量參數(shù)和分子自由度。這幾個參數(shù)都是分子微觀層面的參數(shù),且為常量,不受溫度、壓力等外部條件的影響,可查表獲取。
1
L-J參數(shù)
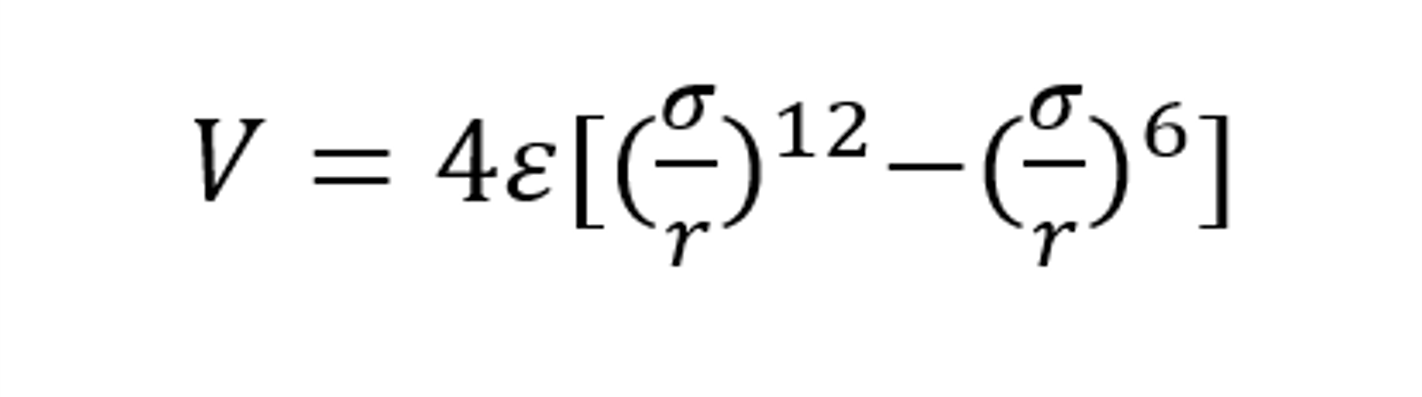
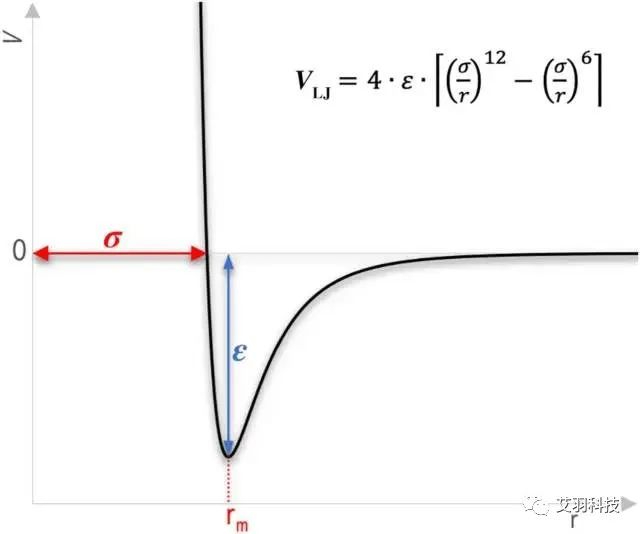
L-J勢和距離的函數(shù)關系
(圖源:《Modified Lennard-Jones potentials for nanoscale atoms》,《Journal of Computational Chemistry》期刊)
在Fluent中,L-J特征長度為 σ(零勢能距離)的數(shù)值,L-J能量參數(shù)為 ε/k(勢阱深度/玻爾茲曼常數(shù))的數(shù)值,其中 k 為玻爾茲曼常數(shù)。需要注意的是,L-J特征長度的單位為angstroms(中文簡稱埃,簡寫為瑞典字符 ?,或者特殊情況下簡寫為英文字母A),其換算為1?=0.1nm。
2
分子自由度
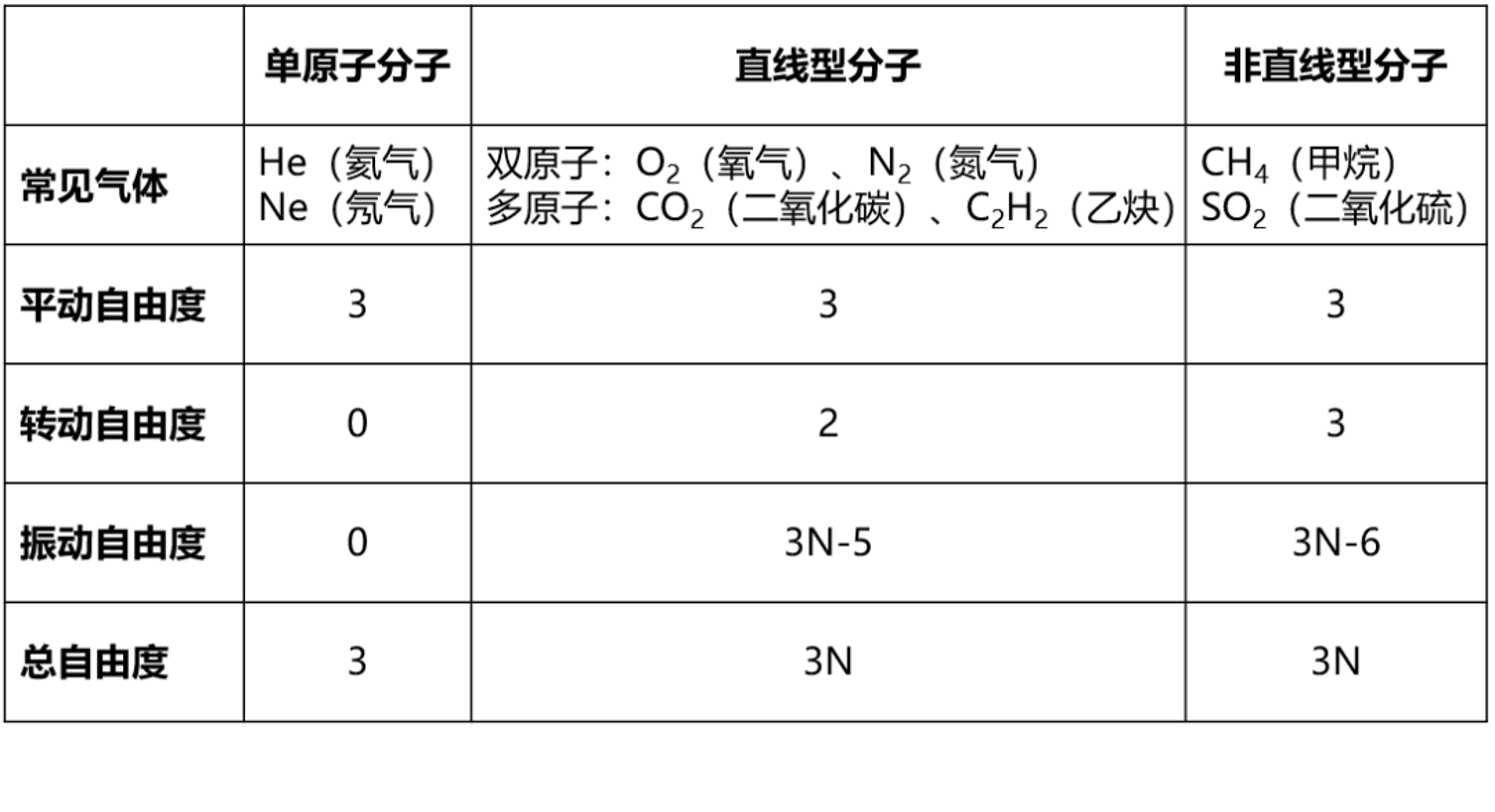
在不太高的溫度下,含有振動自由度的分子比例極低,振動自由度可忽略不計,認為僅包含平動和轉動兩類自由度。溫度升高時,含有振動自由度的分子比例不斷上升,使自由度數(shù)量增加。隨著溫度進一步上升,多數(shù)分子均含有振動自由度,則達到分子自由度的上限3N。
通常的氣體完全激發(fā)振動自由度的溫度(振動特征溫度,characteristic vibrational temperatures)極高。常見的雙原子氣體,僅氯氣的振動特征溫度低于1000K,為805K,其他常見氣體的振動特征溫度均遠高于1000K,例如氮氣為3393K,氧氣2274為K,氫氣為6332K,一氧化碳為3122K。含有多個振動自由度的氣體,每個振動自由度均對應于一個振動特征溫度,不同溫度下可激發(fā)數(shù)量不同的振動自由度,情況更加復雜。
振動特征溫度的計算公式為
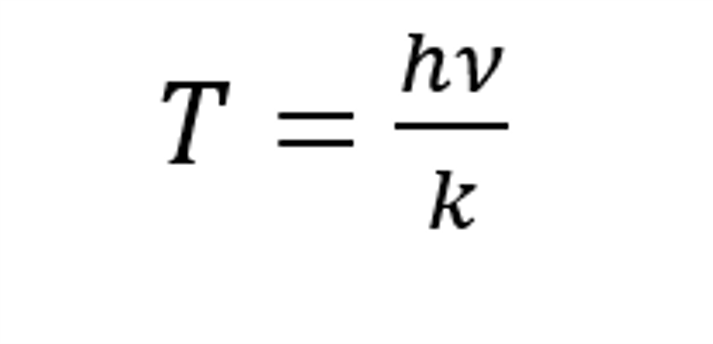
式中,h 為普朗克常數(shù),ν 為分子振動頻率,k 為玻爾茲曼常數(shù)。
1
比熱容
Fluent中比熱容為等壓比熱容。基于理想氣體假設,等壓比熱容和等體積比熱容關系為:
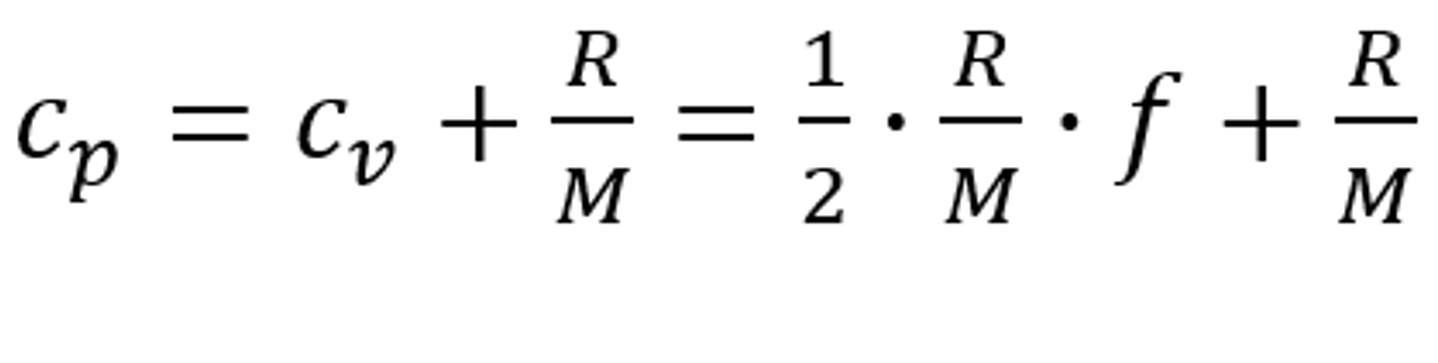
式中,R 為通用氣體常數(shù),M 為氣體分子量,f 為分子自由度
從公式中可以看出,比熱容僅受到分子自由度影響,即受到溫度的間接影響。在室溫附近的較大范圍內(nèi),比熱容可以認為是常數(shù)。
另外,比熱容是唯一需要分子自由度數(shù)據(jù)的材料屬性。
2
粘度
基于Chapman–Enskog理論,結合L-J勢理論,得到以下公式:
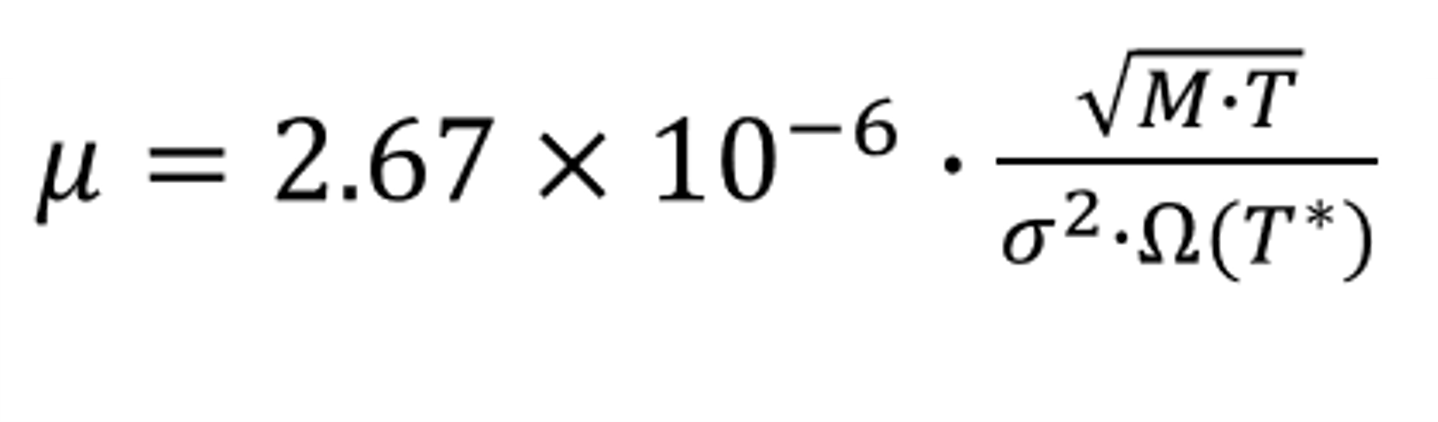
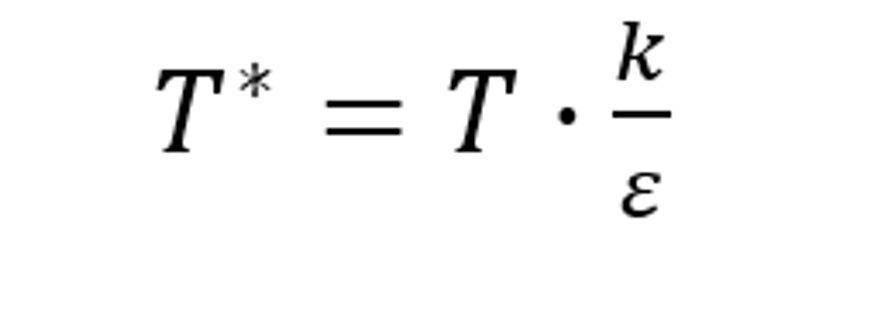
式中,k/ε 為L-J能量參數(shù)的倒數(shù)。
3
熱傳導率
基于Chapman–Enskog理論,結合Arnold Eucken的工作,熱傳導率和比熱容、粘度關系為:
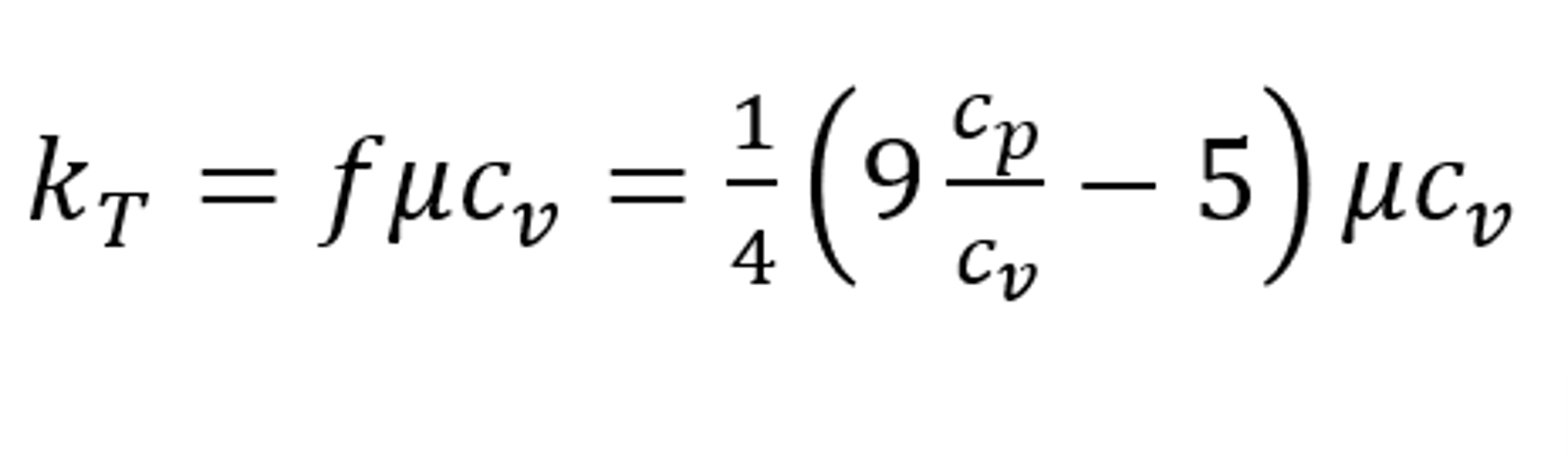
上式結合理想氣體的等壓比熱容和等體積比熱容關系,可得:
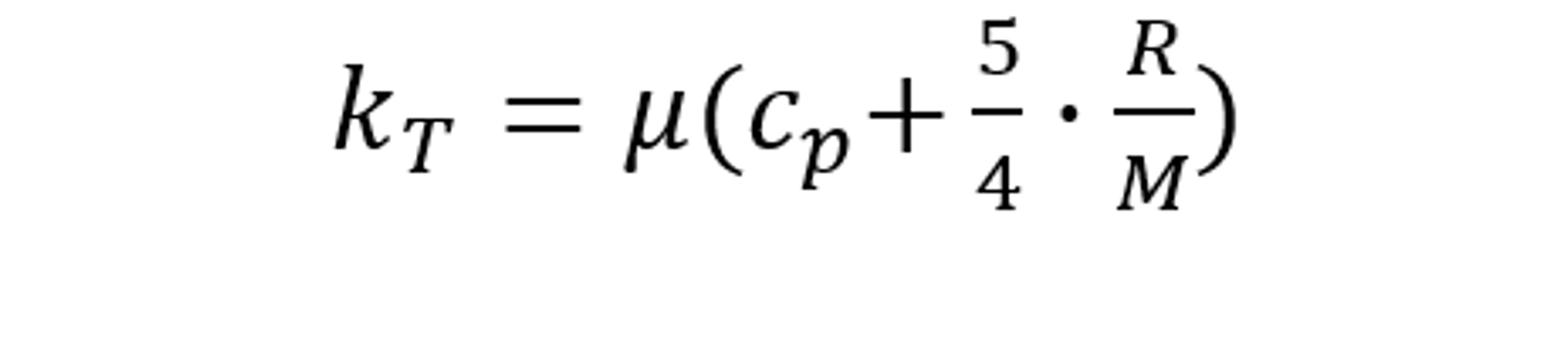
Fluent計算分子動理論定義的熱傳導率,其引用的比熱容和粘度數(shù)據(jù)可以采用常數(shù)、多項式、UDF等其他方法定義,不需要都采用分子動理論方式。
4
質量擴散率
基于Chapman–Enskog理論,混合氣體中任意兩種組分之間的擴散率為:
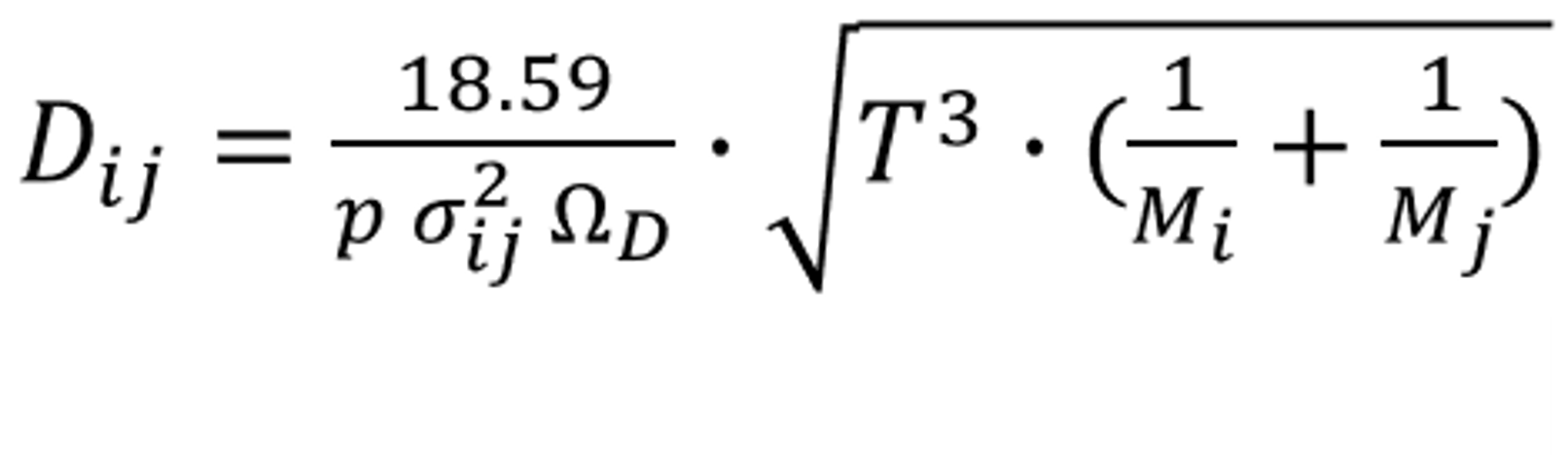
式中,p 為絕對壓力, σij 為組分的L-J特征長度的函數(shù),定義為:
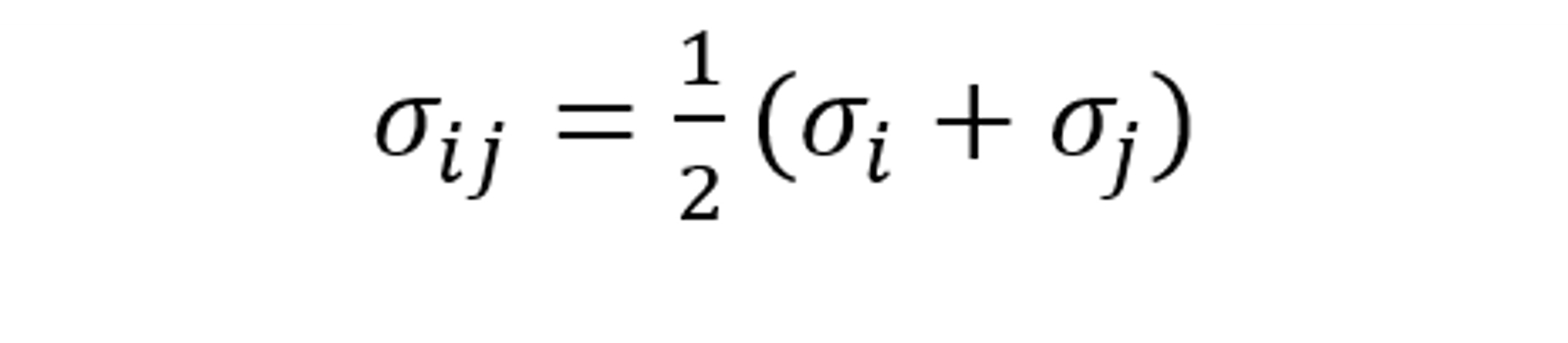
ΩD 為擴散碰撞積分函數(shù),其表達式為:
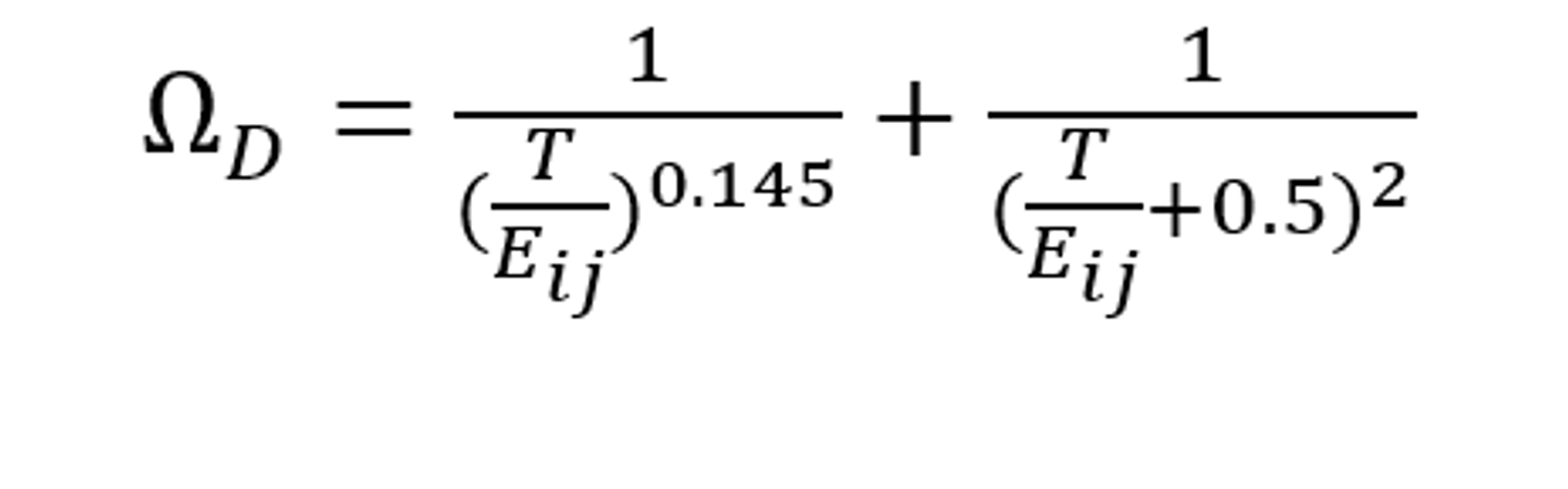
其中,Eij 是組分的L-J能量參數(shù)的函數(shù),定義為:
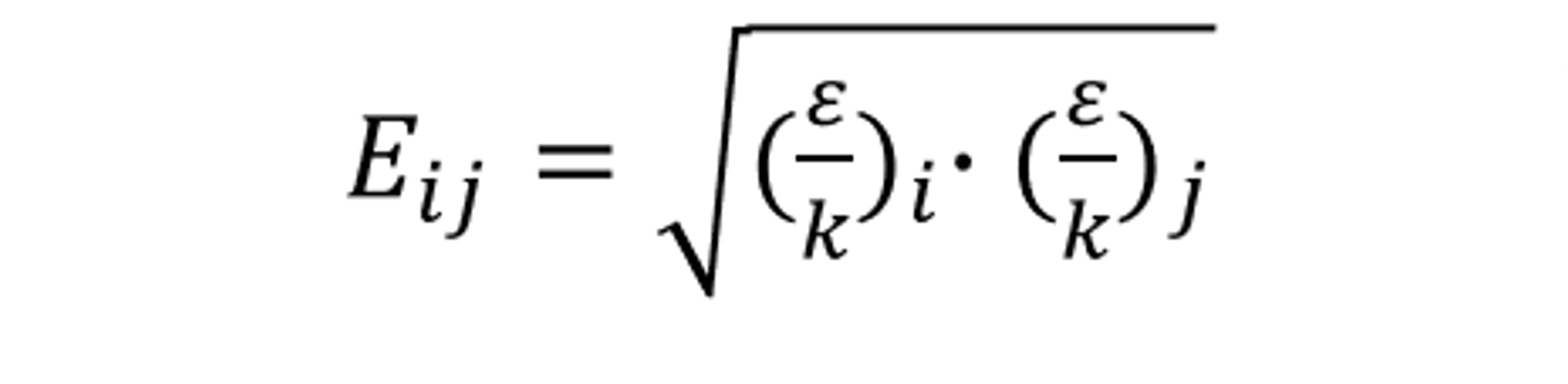
式中,ε/k 為組分的L-J能量參數(shù)。